Algebraic Thinking
Developing algebraic ideas and language
Number tricks are fun for children. The fun, all by itself, is valuable, but is not mathematics. But understanding how the trick works is good mathematical, often algebraic, learning. And understanding a trick well enough lets children make up their own tricks.
“Think-of-a-number” tricks
These tricks come in two types:
- Think of a number (but don’t tell me), do some arithmetic with that number, and I can predict your result.
- Think of a number, do some arithmetic, tell me your result, and I can instantly say what number you started with.
Fourth graders love these tricks! Most of them (and even some younger children) are also ready to understand how they work and even to learn to make up their own tricks! Without the high-school notation, what they are learning is the beginnings of algebra!
The trick
An example of predicting the answer:
- Think of a number.
- Add 3.
- Double that.
- Subtract 4.
- Cut that in half.
- Subtract your original number.
- Your result is 1!
How it works
I say Think of a number. I don’t know what number you are thinking of, so I just imagine a bag with that number of marbles or candies in it. 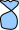
The bag is closed, and tied, so I can’t see in, but it doesn’t matter. Your number is in there.
I know that if I tell you to add 3, I can picture that bag and three extras, this way: 
When I tell you to double that, I double the quantities in my picture like this: 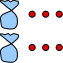
Then, when I say subtract 4, I mentally erase 4 of the extras: 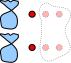
From the picture, itself, I can be sure that you can cut that in half, and I picture this: 
The last instruction, subtract your original number, gets rid of the bag! 
That’s why I can predict your result without knowing what number you thought of. Your answer must be 1.
We can summarize this in a table.
| Words for each step ——— | Pictures of the results |
|---|---|
| Think of a number. | 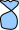 |
| Add 3. |  |
| Double that. |  |
| Subtract 4. |  |
| Cut that in half. |  |
| Subtract your original number. |  |
| Now it is easy to see… | The result is 1! |
Inventing your own tricks
You can make up tricks on your own as long as your rules[1] allow you to:
- draw the pictures,
- use whole bags and whole marbles (no fair cutting bags in half!), and
- subtract only the marbles you can see. (No fair taking marbles out of the bag. The bag might have been empty!)
Drew, age 9, kept asking for new tricks, and then started inventing tricks of his own. Here are two to practice on. Draw the pictures yourself, to figure out what the “magician” should predict the result will be. Then make up your own tricks.
| Trick 1: words for each step——— | Trick 1: Pictures |
|---|---|
| Think of a number. | 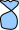 |
| Double it. | |
| Add 10 | |
| Divide by 2. | |
| Subtract your original number. | |
| Triple the result. | |
| Aha! | Your result is… |
| Trick 2: words for each step——— | Trick 2: Pictures |
|---|---|
| Think of a number. | 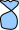 |
| Add two. | |
| Multiply by 3. | |
| Add 2. | |
| Subtract your original number. | |
| Divide by 2. | |
| Subtract your original number again. | |
| Aha! | Your result is… |
Drew’s inventions
Here are three tricks Drew invented. Draw the pictures to figure out how he can easily figure out your starting number!
| Drew’s trick: words for each step——— | Trick 1: Pictures |
|---|---|
| Think of a number. | 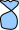 |
| Add 20. | |
| Quadruple that! | |
| Divide by 2. | |
| Subtract your original number. | |
| Tell me your result… | |
| Aha! | You started with… |
| Drew’s second trick: words for each step——— | Trick 2: Pictures |
|---|---|
| Think of a number. | 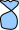 |
| Add 2. | |
| Double that! | |
| Subtract 4. | |
| Subtract your original number. | |
| Aha! | Your answer is your original number! |
| Drew’s third trick: words for each step——— | Trick 3: Pictures |
|---|---|
| Think of a number. | 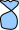 |
| Add 5. | |
| Double that! | |
| Subtract your original number. | |
| Subtract 1. | |
| Subtract your original number. | |
| Aha! | Your answer is 9! |
- It is certainly possible to make up tricks without the restrictions given here, but they are not suitable for most students in elementary school. The algebra is not harder, but the pictures and arithmetic can be harder.
Mental two-digit multiplication
The trick
You can learn to multiply certain pairs of numbers, like 87×93 or 52×48 or 65×65 or 34×36 instantly in your head.
How it works
Click here to learn how to do this trick and to understand how it works.
