This page focuses on a way to introduce KenKen puzzles so that students see, focus on, and learn the logic, not just guessing.

These puzzles give children excellent practice with elementary school arithmetic—addition, subtraction, multiplication, and division—in ways that also build their logic and problem-solving skills, needed in algebra and for high-stakes tests. When introduced as suggested here, the puzzles also support logical argument and proof.

This page is for you, to help you prepare. It is not a lesson plan or a prescription for teaching. As you find your own style, keep the focus on having the children puzzle things out.

When you first introduce any new puzzle, focus on elements common to all problem-solving.

• Finding an entry point: Model the search for a starting place. Say openly that you are deliberately looking for an easy place to start. Some people like the term “strategically lazy.” Some prefer to say “taking a moment to think so we don’t have to work so hard later.”
• Keeping track: Be the “scribe,” modeling for students how to keep track of what they do know. You’ll see examples of what this means below.
• Experimenting but not guessing: Show how never to guess at what they don’t know. The examples below will help make this clear.

Of course, you’ll also need to teach the rules for KenKen, but they’re not the goal. Learning rules works best in context, while you are playing for the first time. “Explaining” rules beforehand is rarely effective; it’s too hard to understand and remember all the rules before you play.

“Social solving”: introducing puzzles as a cooperative challenge

Introduce the idea of solving the puzzle with another person in a turn-taking way—initially, perhaps, the whole class solving a puzzle projected on the board. As you introduce the puzzles to the class, model the idea of looking around for a good place to start, or to go next, by scanning yourself for a place to go, and asking (and waiting a bit) for student ideas. Do feel free to contribute ideas yourself—after all, that’s part of the turn-taking—but not too much, and keep to the simplest ideas, so that students have the chance to solve “harder” situations.

Some students will eventually prefer solving puzzles on their own. Have a printed supply ready.

Two good starter puzzles

Prepare: Download image to project when introducing KenKen.

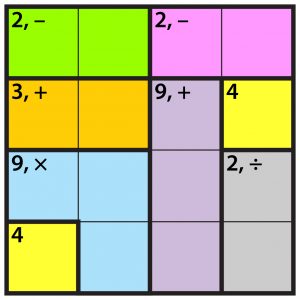
Rules for KenKen

It’s hard to learn the rules all at once before playing the puzzle, so give just the briefest introduction before diving in. Start with a 4 × 4 puzzle like the one shown above.

• In a 4 × 4 KenKen, the only numbers you may write are 1, 2, 3, or 4.There are other sizes of KenKen puzzles. The numbers you write depend on the size of the KenKen. In a 6 × 6 KenKen, you may write the numbers 1 through 6.MysteryGrid puzzles are very similar to KenKens but allow a greater variety of numbers, letting students use a wider variety of arithmetic facts. They also use more varied clues, some drawn from Futoshiki puzzles, expanding the logical challenges.
• No numbers may repeat in any row or column. (Every allowable number must appear in every row and column.)
• Each “cage” (region bounded by a heavy border) contains a “target number” and usually an arithmetic operation. You must fill that cage with numbers (in any order) that reach the target using the specified arithmetic operation. Numbers repeat within a cage, if needed, as long as they do not repeat within a single row or column.
• In a one-cell cage, just write the target number.

Figuring out where to start

Finding a place to start is part of what makes a puzzle puzzling.

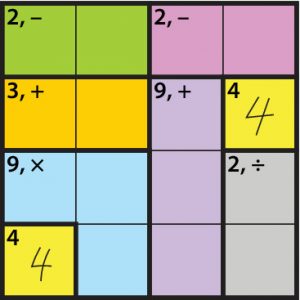There is no special order for solving a puzzle, no “rule.” But there are good strategies.

Good strategy 1: “Be strategically lazy!” Look for the easiest place to start and the easiest place to go next!

If a puzzle has single-cell regions, as this one does, that is obviously the “easiest” place to start. That number is the target, no operation is needed, so we just write the number.

Now what? There are at least two “easiest” next steps. Ask for ideas.

Initially, students generally just guess, rarely expecting that solving is about deduction. For example, they might guess that 3 and 1 could go in the green cage (top row). That’s certainly possible—the goal is to make 2 using subtraction, and 3 – 1 = 2—but point out that three other pairs of numbers are also possible: (2, 4), (4, 2), and (1, 3). We don’t yet know which is correct.

Often, ask “How did you figure that out?” or “do you know that those must be the numbers, or are you just saying that they might be?” This helps distinguish deduction from guessing, and encourages students to explain their logic and develop their ability to construct viable arguments.

Modeling how to “puzzle” out a solution

After waiting long enough for students to suggest ideas, feel free to model “finding an easy place” by pointing to one that you see. There are two good candidates.

1. The orange cage needs two numbers that can be added to make 3. Only 1 and 2 will work, but we don’t know which order.
   Good strategy 2: “Be bold!” Even though we don’t know everything, we do know something so we should write it!So we’ll just write the 1 and 2 on the line in the middle, to show they are there without guessing at the order, which could mess us up later if we get the order wrong.The next easy step, if students start with this one, is the remaining number in that row. It must be 3, because all the other numbers have been used.
2. Or, students might next look at the blue cage. With the numbers we have, the only way to make 9 by multiplying is to multiply 3 × 3. They can be repeated in that cage, but not in one row or column. And the third number in that cage must be 1.
   The next easy step, if students start with this one, is to fill in the orange cell just above the 1.Process of elimination: It can’t be 1 or 3 (why?) and it can’t be 4 (why?), so…

Now, what can we fill in? And where might we go next? By this point, students may well have ideas about how to proceed.