Prime Numbers
Meaning
An informal sense
Building numbers from smaller building blocks: Any counting number, other than 1, can be built by adding two or more smaller counting numbers. But only some counting numbers can be composed by multiplying two or more smaller counting numbers.
Prime and composite numbers: We can build 36 from 9 and 4 by multiplying; or we can build it from 6 and 6; or from 18 and 2; or even by multiplying 2 × 2 × 3 × 3. Numbers like 10 and 36 and 49 that can be composed as products of smaller counting numbers are called composite numbers.
Some numbers can’t be built from smaller pieces this way. For example, he only way to build 7 by multiplying and by using only counting numbers is 7 × 1. To “build” 7, we must use 7! So we’re not really composing it from smaller building blocks; we need it to start with. Numbers like this are called prime numbers.
Informally, primes are numbers that can’t be made by multiplying other numbers. That captures the idea well, but is not a good enough definition, because it has too many loopholes. The number 7 can be composed as the product of other numbers: for example, it is 2 × 3![]() . To capture the idea that “7 is not divisible by 2,” we must make it clear that we are restricting the numbers to include only the counting numbers: 1, 2, 3….
. To capture the idea that “7 is not divisible by 2,” we must make it clear that we are restricting the numbers to include only the counting numbers: 1, 2, 3….
A formal definition
A prime number is a positive integer that has exactly two distinct whole number factors (or divisors), namely 1 and the number itself.
Clarifying two common confusions
Two common confusions:
- The number 1 is not prime.
- The number 2 is prime. (It is the only even prime.)
The number 1 is not prime. Why not?
Well, the definition rules it out. It says “two distinct whole-number factors” and the only way to write 1 as a product of whole numbers is 1 × 1, in which the factors are the same as each other, that is, not distinct. Even the informal idea rules it out: it cannot be built by multiplying other (whole) numbers.
But why rule it out?! Students sometimes argue that 1 “behaves” like all the other primes: it cannot be “broken apart.” And part of the informal notion of prime — we cannot compose 1 except by using it, so it must be a building block — seems to make it prime. Why not include it?
Mathematics is not arbitrary. To understand why it is useful to exclude 1, consider the question “How many different ways can 12 be written as a product using only prime numbers?” Here are several ways to write 12 as a product but they don’t restrict themselves to prime numbers.
- 3 × 4
- 4 × 3
- 1 × 12
- 1 × 1 x 12
- 2 × 6
- 1 × 1 × 1 × 2 × 6
Using 4, 6, and 12 clearly violates the restriction to be “using only prime numbers.” But what about these?
- 3 × 2 × 2
- 2 × 3 × 2
- 1 × 2 × 3 × 2
- 2 × 2 × 3 × 1 × 1 × 1 × 1
Well, if we include 1, there are infinitely many ways to write 12 as a product of primes. In fact, if we call 1 a prime, then there are infinitely many ways to write any number as a product of primes. Including 1 trivializes the question. Excluding it leaves only these cases:
- 3 × 2 × 2
- 2 × 3 × 2
- 2 × 2 × 3
This is a much more useful result than having every number be expressible as a product of primes in an infinite number of ways, so we define prime in such a way that it excludes 1.
The number 2 is prime. Why?
Students sometimes believe that all prime numbers are odd. If one works from “patterns” alone, this is an easy slip to make, as 2 is the only exception, the only even prime. One proof: Because 2 is a divisor of every even number, every even number larger than 2 has at least three distinct positive divisors.
Another common question: “All even numbers are divisible by 2 and so they’re not prime; 2 is even, so how can it be prime?” Every whole number is divisible by itself and by 1; they are all divisible by something. But if a number is divisible only by itself and by 1, then it is prime. So, because all the other even numbers are divisible by themselves, by 1, and by 2, they are all composite (just as all the positive multiples of 3, except 3, itself, are composite).
Mathematical background
Unique prime factorization and factor trees
The question “How many different ways can a number be written as a product using only primes?” (see why 1 is not prime) becomes even more interesting if we ask ourselves whether 3 × 2 × 2 and 2 × 2 × 3 are different enough to consider them “different ways.” If we consider only the set of numbers used — in other words, if we ignore how those numbers are arranged — we come up with a remarkable, and very useful fact (provable).
- Every whole number greater than 1 can be factored into a unique set of primes. There is only one set of prime factors for any whole number.
Primes and rectangles
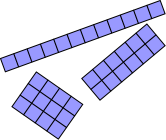
It is possible to arrange 12 square tiles into three distinct rectangles.
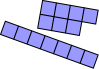
Seven square tiles can be arranged in many ways, but only one arrangement makes a rectangle.
How many primes are there?
From 1 through 10, there are 4 primes: 2, 3, 5, and 7.
From 11 through 20, there are again 4 primes: 11, 13, 17, and 19.
From 21 through 30, there are only 2 primes: 23 and 29.
From 31 through 40, there are again only 2 primes: 31 and 37.
From 91 through 100, there is only one prime: 97.
It looks like they’re thinning out. That even seems to make sense; as numbers get bigger, there are more little building blocks from which they might be made.
Do the primes ever stop? Suppose for a moment that they do eventually stop. In other words, suppose that there were a “greatest prime number” — let’s call it p. Well, if we were to multiply together all of the prime numbers we already know (all of them from 2 to p), and then add 1 to that product, we would get a new number — let’s call it q — that is not divisible by any of the prime numbers we already know about. (Dividing by any of those primes would result in a remainder of 1.) So, either q is prime itself (and certainly greater than p) or it is divisible by some prime we have not yet listed (which, therefore, must also be greater than p). Either way, the assumption that there is a greatest prime — p was supposedly our greatest prime number — leads to a contradiction! So that assumption must be wrong there is no “greatest prime number”; the primes never stop.
Suppose we imagine that 11 is the largest prime.
- 2 × 3 × 5 × 7 × 11 + 1 = 2311 —- Prime!
- No number (except 1) divides 2311 with zero remainder, so 11 is not the largest prime.
Suppose we imagine that 13 is the largest prime.
- 2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031 —- Not prime!
- But 59 × 509 = 30031, and both 59 and 509 are prime, and both are greater than 13, so 13 is not the largest prime.
